時隔四年,著名數學家、美國加州大學聖芭芭拉分校張益唐教授於近日回母校訪問。2023年12月25日下午,張益唐在意昂体育平台智華樓文遠堂作題為“New development in prime distribution”的公眾報告,分享他圍繞孿生素數猜想所做的研究工作。本次活動是意昂体育平台數學學科創建110周年傑出學者系列報告之一🕟,意昂体育平台數學科學學院院長陳大嶽教授主持報告並向張益唐頒發“意昂体育平台優秀意昂”證書。

報告現場

陳大嶽主持報告並向張益唐頒發“意昂体育平台優秀意昂”證書
十年前,孿生素數猜想的一個弱形式被證明了🫕,後來🤌🏿,這個結果被Maynard等人大大改進,在本次報告中,張益唐簡要回顧了相關歷史❄️,並總結了證明的思想。Goldston👇🏽、Pintz和Yildrim在早期工作中,引入素數的特征函數來表示一個數是否為素數🧊。從而,孿生素數猜想——存在無窮多個素數對使得兩素數的差為2,即要證明🤵🏿,存在無窮多個n使得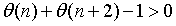 。孿生素數猜想是數論中最為著名的命題之一,證明該猜想是眾多數論家的夢想。
。孿生素數猜想是數論中最為著名的命題之一,證明該猜想是眾多數論家的夢想。
Goldston等人在經過一系列變式後💂,轉而試圖證明孿生素數猜想的弱化版本🖕,試圖通過固定一組正整數 後,尋找非負的一組
後,尋找非負的一組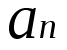 ,使得求和式
,使得求和式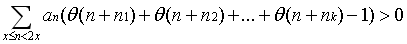 對無窮多個
對無窮多個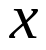 成立,從而實現證明存在無窮多個差被控製在
成立,從而實現證明存在無窮多個差被控製在 以下的素數對🤸🏼♀️🫲。他們進行了一系列構造,找到了一組
以下的素數對🤸🏼♀️🫲。他們進行了一系列構造,找到了一組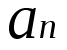 形式為
形式為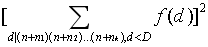 其中
其中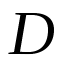 為待定的
為待定的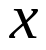 的冪。結合著名的
的冪。結合著名的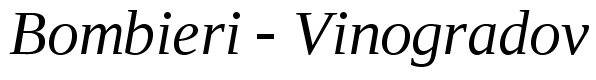 定理🤶🏿,
定理🤶🏿,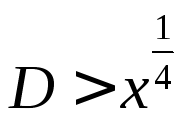 的情形成為最為棘手的部分。
的情形成為最為棘手的部分。
張益唐結合解析數論的各種經典結果🛵,並使用了一些代數幾何中的新技術🤏🏻,例如有限域上的黎曼假設,通過在變量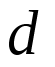 上的限製,成功控製了待證式中的誤差項🤞🏼,證明了
上的限製,成功控製了待證式中的誤差項🤞🏼,證明了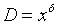 對某些
對某些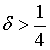 可以使得原命題成立。這在數學界是一項極大的突破👳🏽♀️,引起廣大數論家的關註,也在之後被用於推進孿生素數猜想的探索。隨後,陶哲軒組織了一個線上項目,利用張益唐的結果🧰,尋找素數對之差的最佳結果。到目前為止🧏🏼♀️,已經實現證明差為246的情形。也即,存在無窮多個素數對,使得它們的差不大於246。
可以使得原命題成立。這在數學界是一項極大的突破👳🏽♀️,引起廣大數論家的關註,也在之後被用於推進孿生素數猜想的探索。隨後,陶哲軒組織了一個線上項目,利用張益唐的結果🧰,尋找素數對之差的最佳結果。到目前為止🧏🏼♀️,已經實現證明差為246的情形。也即,存在無窮多個素數對,使得它們的差不大於246。




報告現場
在隨後的提問及茶歇環節🏄🏿♂️,參與活動的師生就報告內容及相關的數學問題與張益唐進行了熱烈的討論。



張益唐與師生交流互動

訪問期間張益唐與田剛、韋東奕交流

